30 Nov 23
Different ways to prevent overfitting in machine learning: Navigating the Thin Line
In this Article
In the rapidly evolving landscape of machine learning, the pursuit of accuracy often leads developers and data scientists to confront a significant challenge: overfitting. While the ultimate goal is to create models that generalise well to new, unseen data, overfitting is a two-pronged problem which gives the illusion of accuracy while in turn producing less meaningful results. In this blog, we’ll delve into the various ways to prevent overfitting in machine learning. Whilst exploring overfitting’s consequences, and examining its intricacies.
Understanding Overfitting & ways to prevent overfitting in machine learning

At its core, overfitting occurs when a machine learning model learns the training data too well, capturing not only the underlying patterns but also the noise and fluctuations inherent in that specific dataset. Consequently, an overfitted model performs exceptionally well on the training data but fails to generalise effectively to new, unseen data. It essentially memorises the training set instead of learning the underlying patterns that would enable it to make accurate predictions on diverse datasets. Employing multiple ways to prevent overfitting in machine learning is crucial to ensure that the model doesn’t merely memorise the training data but rather learns the essential patterns for making accurate predictions in various scenarios. It is analogous to revising for an exam by simply memorising all the questions and answers from the practice papers – while you may get 100% on the practice papers, you have not learnt how to actually solve any exam questions and so will do badly in the exam.
One of the easiest ways to prevent overfitting in machine learning is to consider doing polynomial linear regression in two dimensions. This machine-learning method attempts to find the equation of a line which goes through as many data points as possible. Consider the following dataset.
| X | Y |
| 1 | 10 |
| 2 | 12 |
| 3 | 14 |
| 4 | 16 |
It is easy to spot the pattern and indeed the equation for the linear regression line is Y = 2X + 8. On the data this equation perfectly predicts each data point. Now consider the following data which is very similar but with some slight fluctuations added.
| X | Y | Y (predicted) | Error |
| 1 | 10.1 | 10 | 0.1 |
| 2 | 11.9 | 12 | 0.1 |
| 3 | 14.05 | 14 | 0.05 |
| 4 | 16.05 | 16 | 0.05 |
If we use the same model, the equation still performs very well. The mean squared error of using the same equation is 0.00625, which is a very low error term. Now let’s consider using a model which is overfitted. Any set of n points of data can theoretically be hit by a polynomial of degree n-1. In this case that would be a cubic polynomial. The cubic equation which hits all these datapoints is -1/12 x^3 + 27/40 x^2 + 43/120 x + 9.15. Immediately we can see that the equation is far more complex, and it is not immediately clear what the relationship is between X and Y is. This equation technically performs better with a mean squared error of 0, but let’s plot both equations and see what happens when the X values go beyond the training data range.
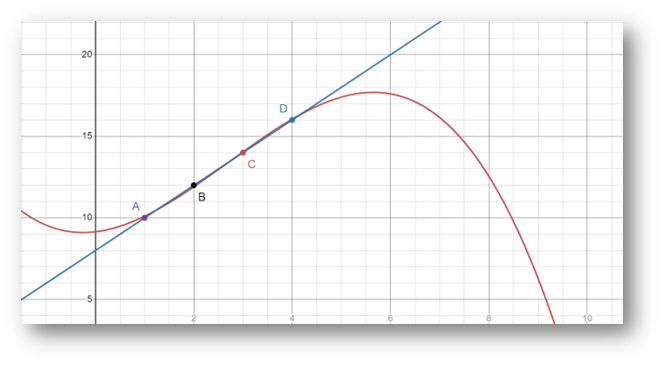
The graph makes it even clearer that the more complex equation differs severely from the original equation. As the X values deviate more and more from the range in the sample set, the Y values become more and more extreme. The slight increase in accuracy for the training data has been offset by the massive loss in accuracy for unseen values. This is the fundamental problem with overfitting.
Another factor to consider in addressing ways to prevent overfitting in machine learning is the increased computational demand during model training to achieve high accuracy. The simple example above illustrates how complex the equations can get. Calculating the polynomial interpolation of a dataset has computational complexity of O(n2), meaning that if the dataset doubles in size, then the computing time needed to train the model will multiply by 4. The resource drain for such models will grow incredibly quickly while not providing any improvement on the predictions on unseen data.
Different ways to prevent overfitting in machine learning

Cross-Validation
Employing techniques like k-fold cross-validation can help assess a model’s performance on different subsets of the training data. K-fold cross-validation involves splitting all the training data into k subsets. Then, for k iterations, leave one subset out as testing data and train the model on the remining k-1 subsets. The model is then tested on the one unseen subset of the data and an accuracy score is recorded. An average of the accuracy for the k different models is then used as a measure of the accuracy of the whole model. This cross-validation method can highlight and overfitted model as if it performs well on the whole dataset but not when trained on subsets of the data, the model has been overfit and will not generalise well. However, this is just one of the ways to prevent overfitting in machine learning.
Regularisation Techniques:
Regularisation methods, such as L1 and L2 regularisation, introduce penalties for complex models. These techniques discourage the model from assigning undue importance to certain features, and is one of the ways to prevent overfitting in machine learning. It promotes simpler and more generalizable models. In our example, the more complex model would have a penalty introduced for including the X2 and the X3 terms.
Data Augmentation:
Augmenting the training dataset by introducing variations and perturbations to the existing data can enhance a model’s ability to generalise. This technique exposes the model to a broader range of scenarios, reducing its reliance on specific training examples and causing it to learn the overall trends of the training data instead of learning the specific values.
Early Stopping:
Monitoring a model’s performance on a validation set during training and stopping the process when the model’s performance plateaus is one of the ways to prevent overfitting in machine learning. Once the model is already very accurate on the training data, further training is likely to introduce overfitting as the only way for the model to improve is to ‘memorise’ the data.

Navigating the different ways to prevent overfitting in machine learning, is an integral aspect of developing reliable machine-learning models. While the allure of high accuracy on the training set may be tempting, the ultimate success of a model lies in its ability to generalise to new, unseen data. By understanding the causes and symptoms of overfitting and implementing strategies such as cross-validation, regularisation, data augmentation, and early stopping, machine learning engineers can strike a balance between precision and generalisation, ensuring the efficacy of their models in real-world applications. There are multiple ways to prevent overfitting in machine learning, and understanding this ensures a brighter future in the field for anyone who may be on the path.
Interested in joining our diverse team? Find out more about the Rockborne graduate programme here.
Related posts
Life at Rockborne20 Jun 25
Federated Learning: The Future of Collaborative AI in Action
Federated Learning: The Future of Collaborative AI in Action The way we build, deploy, and govern AI is evolving, and so are the expectations placed on organisations to do this...
09 Sep 24
Tips to Succeed in Data Without a STEM Degree
By Farah Hussain I graduated in Politics with French, ventured into retail management, dabbled in entrepreneurship, a mini course in SQL and now… I am a Data Consultant at Rockborne....
15 Apr 24
Game Development at Rockborne: How is Python Used?
Just how is Python used in game development? In this blog post, we see the Rockborne consultants put their theory into practice. As the final project in their Python Basics...

